丰色 发自 凹非寺

量子位 | 公众号 QbitAI

不到一个月的时间，陶哲轩又一篇论文上线：

这次是关于欧拉函数的单调非递减序列，他通过初等论证证明了一个名为M(x)函数的渐近式。

（即随着x增大，M(x)的行为趋势）

该函数在他之前的一篇博客中有所提及，大意是指一系列从1到x的数字中，满足欧拉φ函数是非递减的最长子序列的长度。

毫不意外，这篇论文的出产过程中也用到了AI。

不过，这次陶哲轩承认：

AI工具对他的核心研究并不那么有用（但他也表示可能是不想打破一些已有习惯去尝试）。

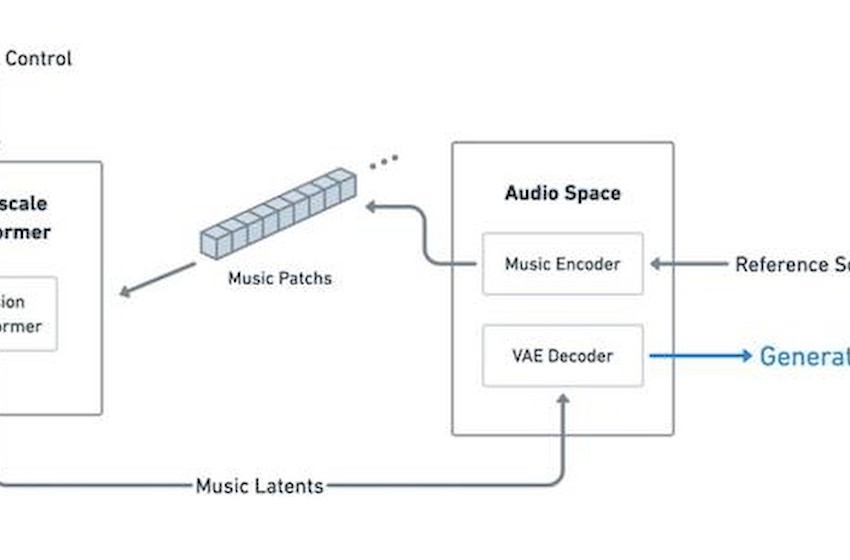
对他帮助最大的其实是编码和生成论文中的流程图初稿。

对于前者，陶哲轩已多次提及。

那么，就来简单看看这次的论文究竟说了什么。

准备长脑子了咳咳。

欧拉函数的单调非递减序列

该论文研究主要涉及函数M(x), 它定义的是数字1到x的最长子序列的长度，在这个子序列中，欧拉函数ψ是非递减的。

（欧拉函数ψ(n)通常用于表示小于或等于n的正整数中与n互质的正整数的数量）

由于M的前几个值是：

所以，举个例子：

M(6)就等于5。

因为欧拉函数在集合{1,2,3,4,5}或{1,2,3,4,6}上是非递减的，在{1,2,3,4,5,6}上不是。

而由于对于任何素数p，ψ(p)=p-1，我们有M(x)≥π(x)。

其中π(x)是素数计数函数（用于表示小于或等于x的正整数中的素数的数量）。

根据经验，这些素数非常接近M(x)的最大长度；Pollack, Pomerance和Treviño已通过数值计算推测出下式

中的x=10⁷ 。

相比之下，以前最著名的上限基本上是以下形式：

对于该式子，在显式常数C=0.81781中，x→∞。

而将该结果与上面的结果相结合，陶哲轩就得到了渐近式：

所以在特殊情况下：

它既回答了Erdős的问题，也回答了与Pollack, Pomerance和Treviño所密切相关的问题。

陶哲轩介绍，该证明所用方法大多数都很基础（解决数论中最先进结果所需的只是带有经典误差项的素数定理）。

基本思想是隔离给定数字1≤n≤x中的一个关键素因子p，因为它对欧拉函数有相当大的影响。

例如，对于“典型”数字n，可以因式分解为：

其中p2是中等大小的素数，p1是明显更大的那个，d则是一个所有素数因子均小于p2的数。这可得出：

因此，如果我们暂时保持d固定，并将n定位到相对较短的区间，那么ψ只能在n中是非递减的——如果p2也同时非递减。

事实证明，特别是在p2很大的情况下，这个方式显著减少了该机制中非递减序列的可能长度。

这个过程可以形式化，达成方式是通过将p的范围划分为各种子区间并检查它 (以及ψ上的单调性假设)如何约束与每个子区间相关联的n值。

而当p2很小时，我们使用因式分解：

其中d非常“平滑”（即没有大素数因子），而p是大素数。我们得到近似值：

并得出结论：为了使ψ不变小，约等式右边的分数基本上必须是分段常数。

再进行一番更仔细的分析之后，我们就能证明初步不等式，最终对于所有正有理数q得到主要定理：

陶哲轩表示，这其实是一个“小奇迹”，与以下事实有关：

公式(4)中分母的大质因数最低项必然等于d的最大质因数，这使得我们能够非常准确地得出公式(5)的左边，从而轻松构建整个公式(5)。

在论文的最后一部分，陶哲轩还讨论了强猜想（1）的一些近似反例，这些例子表明，如果不假设一些“相当强的假设”，可能很难接近证明此猜想。

论文地址：

https://arxiv.org/abs/2309.02325

参考链接：

[1]https://mathstodon.xyz/@tao/111018835694062000

[2]https://terrytao.wordpress.com/2023/09/06/monotone-non-decreasing-sequences-of-the-euler-totient-function/

— 完—

「量子位智库·大模型人才沙龙」招募中

「量子位智库·大模型人才沙龙」将于9月下旬在北京中关村举办，欢迎大模型各领域玩家参与~

点击图片了解详情，企业报名可联系活动负责人王琳玉（微信：iris_wang17，请备注企业+姓名）。

沙龙观众通道后续开放，敬请期待~

点这里👇关注我，记得标星哦～

一键三连「分享」、「点赞」和「在看」

科技前沿进展日日相见 ~